Week 11 - Machine Design
- automate your machine
- document the group project and your individual contribution
- Stepper Motors
- Arduino UNO
- Stepper motors drivers
Softwares :
- Arduino IDE.
- Illustrator.
- Keynote.
- iMovie.
That week was pretty productive ! We made a few prototypes of the drawing machine and improved them. We developed a code that allow to draw straight lines giving the cartesian coordinates of the different nodes of our drawing as input. So to draw a square, we need 4 points. For a letter, we need more. I liked the time spent in small teams with some members of the team. As everybody as different expertise, It's was nice to nourish ourself with these. That also really helped to have coherence in the project. I took on the development of the code as I was the more comfortable with it. The trickiest part was to explain to others what the code was doing so other members of the team could take on the code and be able to improve it. That's the reason I spent some time illustrating what the code was doing. I'm glad other team members could take on the code and adapt it. I must say that these few weeks of group assignment were really energy consuming. But it was worthing it ! We had to learn to listen to each other, to understand each other, to give space to each other which allows us to learn from each other. The temptation to back off and make a small project in your own corner is sometimes there. But it really worths to push and try to make this dream team and live this adventure together. In group, it is inevitable to have lows and highs, but if we believe in it and everybody contributes, we can go very far...
Designing the first prototype
As we decided to go for a drawing machine and after several discussions within the team, we wanted to design a really quick first prototype with Michele. The idea was to have a first prototype on which we could improve and also develop the code.
On several occasions, we discussed in group about the design of our drawing machine. We liked the idea of having two stepper motors on the floor and just some very light spools that we could hold on any wall, or glass window. The idea being that we could draw anything on any surface of any size...
Building the prototype
I discussed with Michele on how we should program our drawing machine. We looked how machine and graphic card were working. We ended on Bresenham's line algorithm. So if we give to points, it is possible to interpolate a line in between the two points.

Michele built the prototype we designed at the speed of light. We are now able to test the code and improve each part of the machine.

Developing the drawing program
Based on the morning discussion with Michele, I set the problem. On the figure here below, the two upper spools are separated by a distance of W. The position of a point (red point) can be expressed in two different sets of coordinates: in cartesian coordinates (x,y) and in the two wires/belts coordinates (a,b). When we control the stepper motors, we control the number of steps which corresponds to the length of the wires a and b. The relation in between the tow sets of coordinates are:
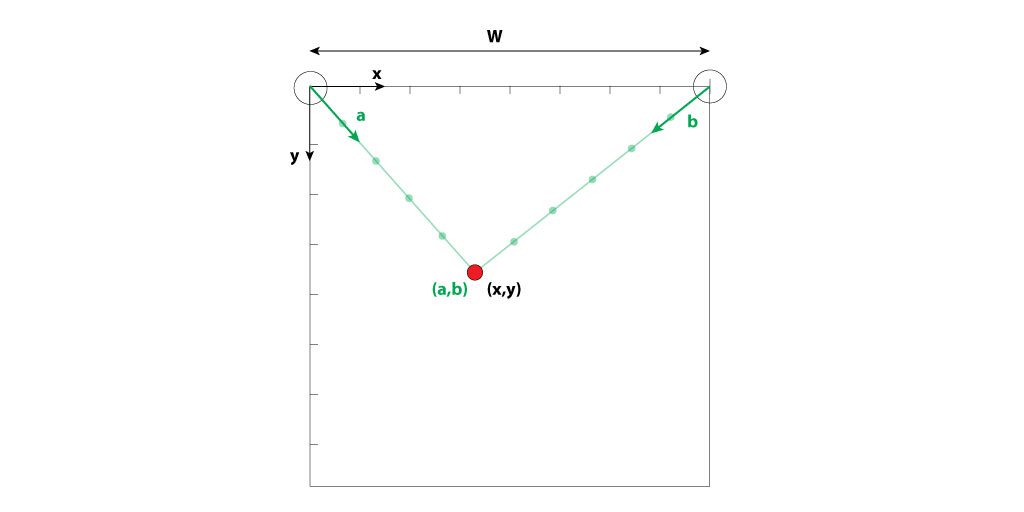
Here is an illustration of a point represented in the 2 sets of coordinates:
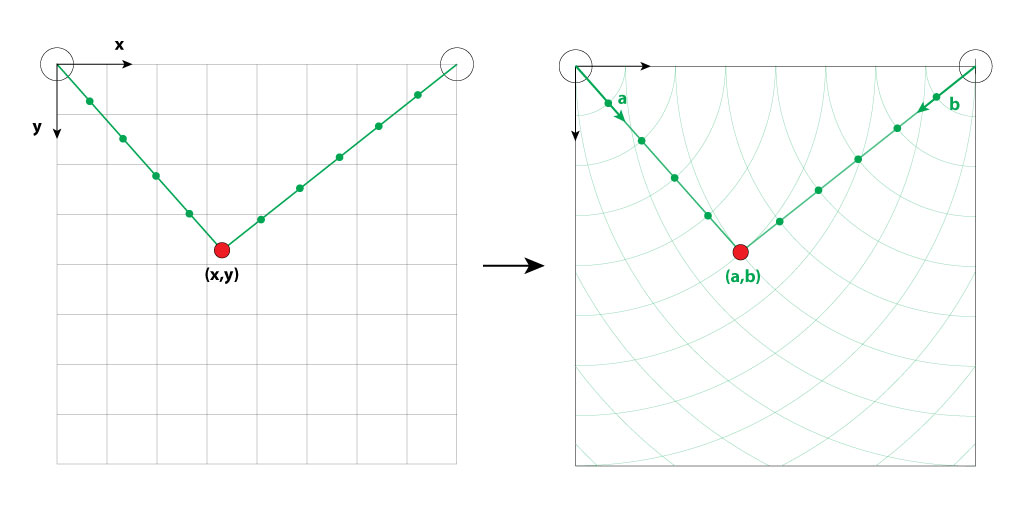
Interpolation of a line in between two points
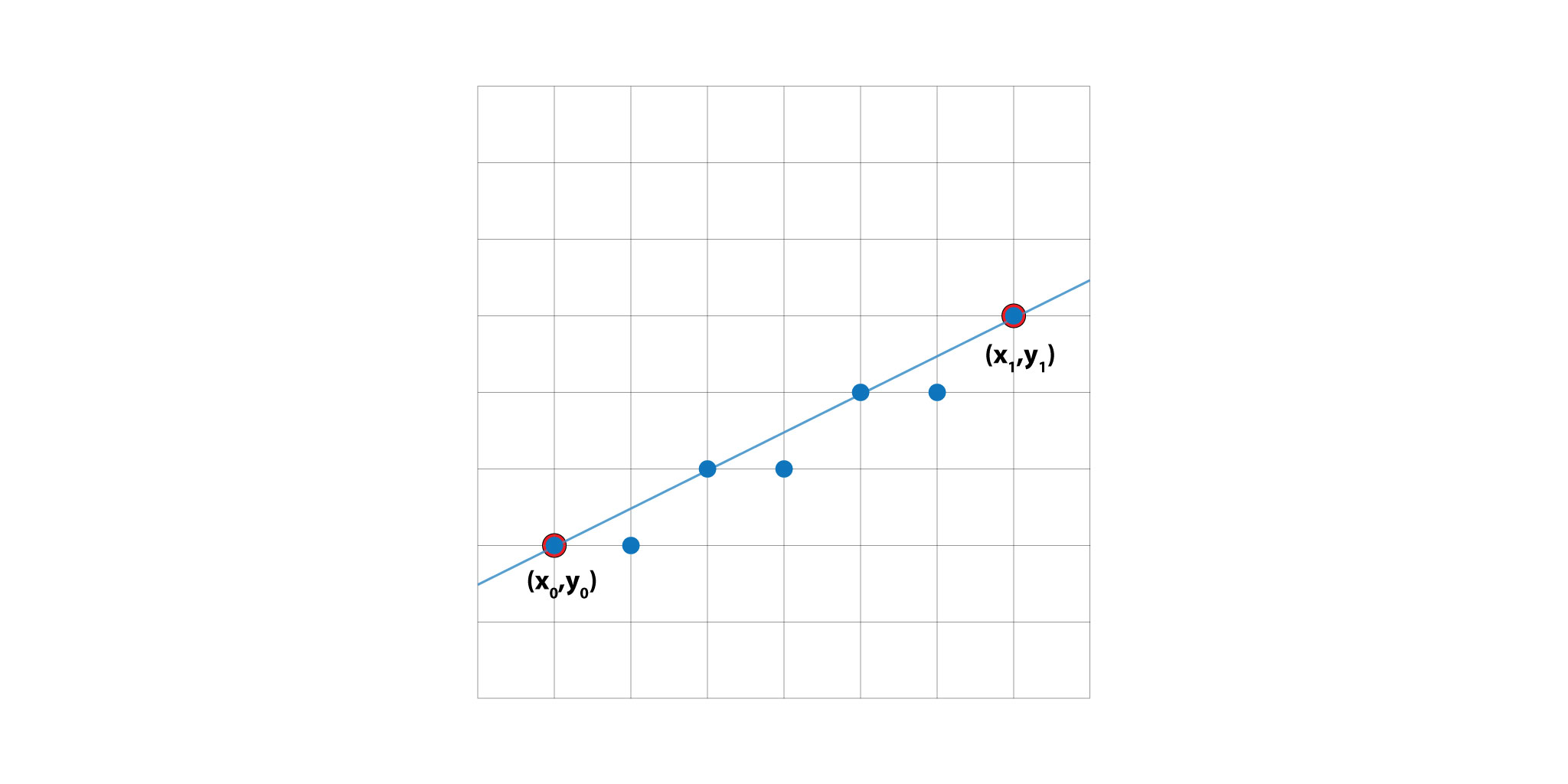
Here is an illustration of the Bresenham's line algorithm. The algorithm finds the closest path to the theoretical lines connecting two points (x_0,y_0) and (x_1,y_1).
Program development - First tests
The stepper motors always move one after the other. So if we want to move form one point to the another, the end effector will produce a drawing that looks like half a rectangle (see the figure exercise 1 down here). If we want to draw an approximately straight line in between the 2 points, we can use the Bresenham algorithm to calculate the series of steps that each motor as to make. Each motor will move one after the other depending on how far the end effector is from the theoretical line.
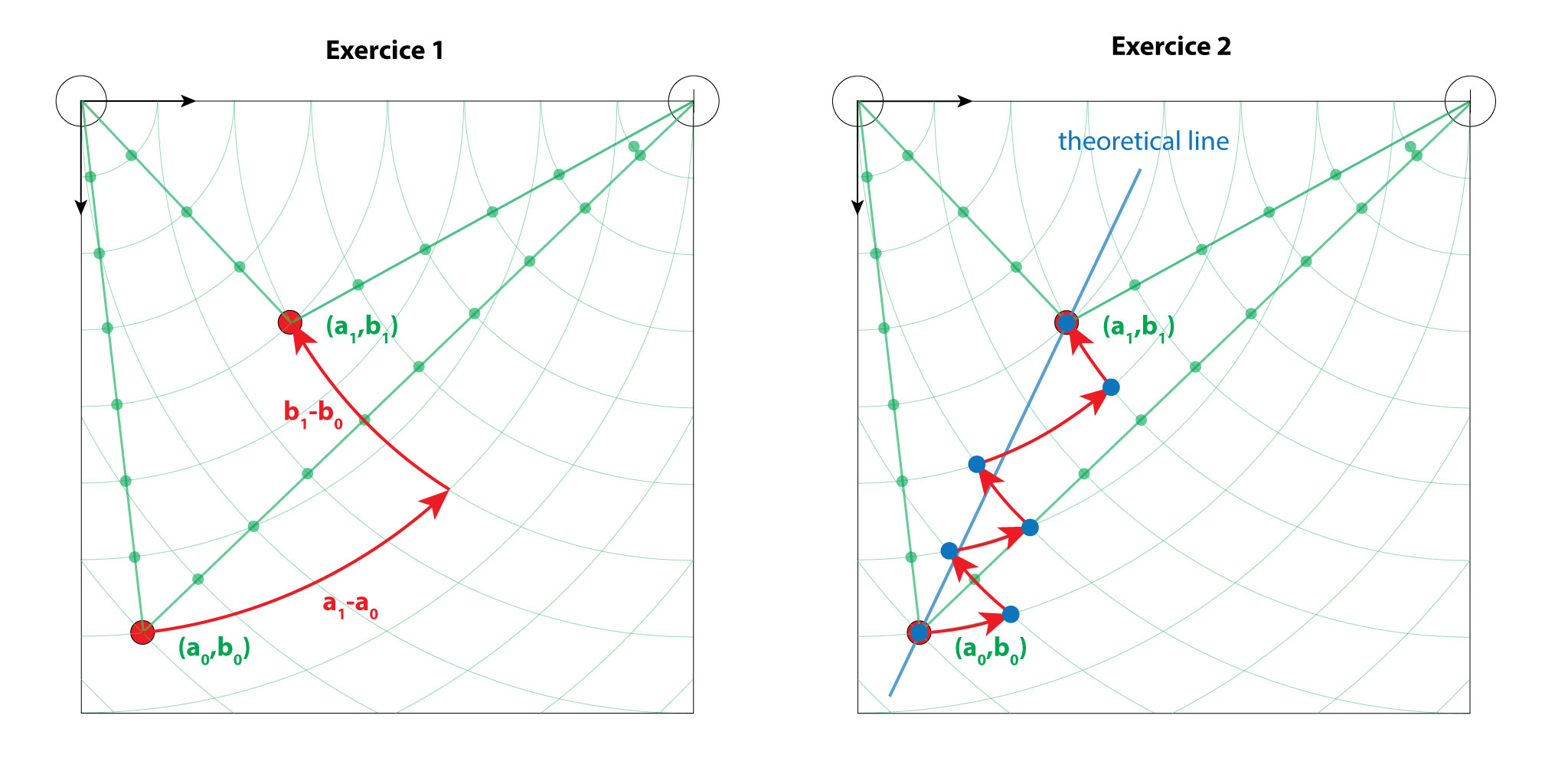
Exercise 1 - From one point to another
Moving between two points back and forth produce something close to a rectangle.
Exercise 2 - Interpolating a line in between two points
For this exercise, we asked the machine to draw straight lines in a zig-zag fashion using the Bresenham algorithm. Zigzags are on purpose !
Exercice 3 - Drawing a square
For this exercice, we asked the machine to draw a square, still using the Bresenham algorithm. Yeah, its working ! We just need to give the absolute cartesian coordinates of the 4 square nodes.
I must admit that this part needed some debugging on my side and perseverance on Michele's and David's side to make the machine do its job !

Exercice 4 - Towards drawing letters
Yes ! The code is working ! The code is able to interpolate in between points and draw the shortest path in between two points. To draw a square, we need 4 points. To draw letters we need more points but with that basis, we should be able to make it.
There was another improvement to make on the code. The lines of the square looked curved. It is because I developed the Bresenham algorithm to work in the belt coordinates. So we would just have to modify the code and let the code make the interpolation in the cartesian coordinates and that should do the trick (and indeed it did).
Presentation video of the making of our drawing machine
I also made the final video and presentation board for the group in keynote and imovie with the assistance of Victor.
