Week 11 - Machine Design

Assignment

		1. Automate your machine


   2. Document the group project
	

Before moving onto automate the machine, it is essential to understand, the basic fundamentals on which the machine works.

For this we have researched, a bit on astronomy, and the calculations which are the backbone to the program.

Astronomy Basics and Principles.

As the basic objective of the machine is to point at celestial bodies automatically.It is essential that we know about their position relative to our own.

Right Ascension and Declination

The celestial bodies are all assigned a constant coordinate, to reference them.How we reference a location on Earth using latitudes and longitudes, the stars too have a sytem known as the right ascension and declination.

The celestial sphere is an imaginary sphere of arbitrarily large radius, concentric with Earth. All objects in the observer's sky can be thought of as projected upon the inside surface of the celestial sphere, as if it were the underside of a dome or a hemispherical screen. The celestial sphere is a practical tool for spherical astronomy, allowing observers to plot positions of objects in the sky when their distances are unknown or unimportant.

The above figure shows how the declination angle would be

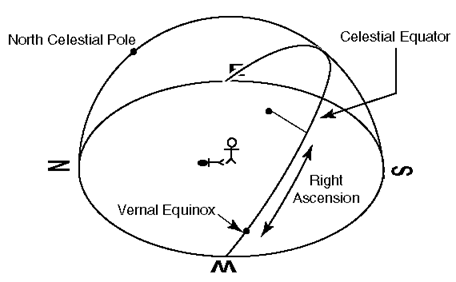
The above figure shows how the Right ascension would be.

The below video helped really well to understand what RA and DEC are.

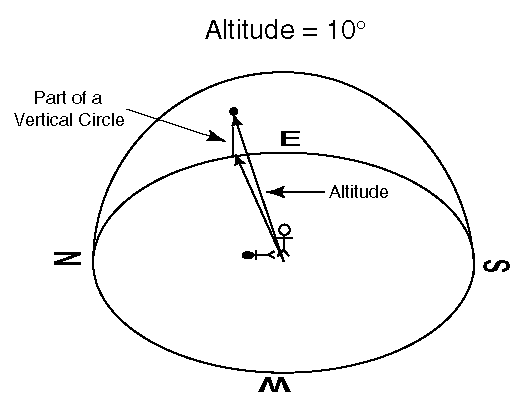
Altitude and Azimuth

Now that we have understood where the celestial body is in the celstial sphere, we need to understand where it is relative to here we are.

Altiude is the corresponding angle to Angle of Declination, in the local sphere.

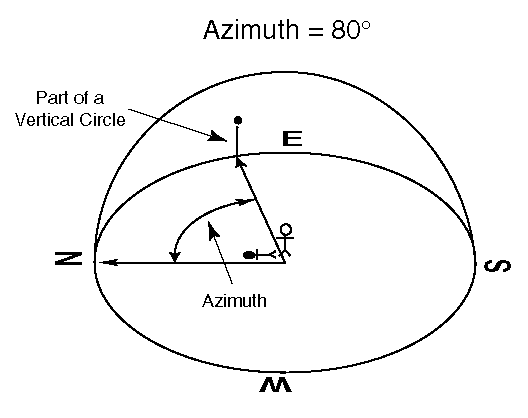
Similarly, the Azimuth corresponds to the Right ascension on the local sphere.

Calculations

The local cordinates has to be calculated from the known celestial cordinates. For that we use the following calculations.

Days since J2000 (d)

Many things (including the siderial time) are measured from fundamental epoch or date. For almost all the modern astronomical purposes, the reference date is J2000, which corresponds to 1200 hrs UT on Jan 1st 2000 AD, and we can use the table provided below to find how many days have gone by since J2000 for any date for the next 20 years or so.

The formulae can be given as
d = number of days from J2000(to current year) + number of days from start of current year to start of current month + number of days in current month + fraction of the day completed (current time/24) // {in 24 hour format}

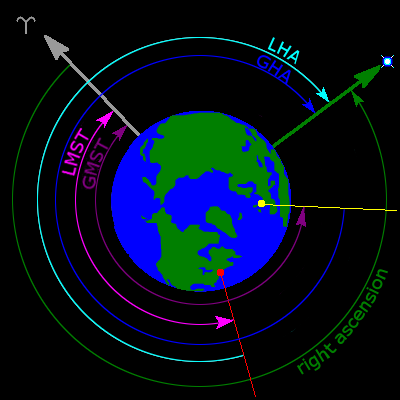
Local Siderial Time

Sidereal time is the hour angle of the vernal equinox, the ascending node of the ecliptic on the celestial equator. The daily motion of this point provides a measure of the rotation of the Earth with respect to the stars, rather than the Sun.

LST = 100.46 + 0.985647 * d + long + 15xUT

• 'd' is the days from J2000, including the fraction of a day
• 'UT' is the universal time in decimal hours
• 'long' is our longitude in decimal degrees, East positive.

Add or subtract multiples of 360 to bring LST in range 0 to 360 degrees.

This formula gives our local siderial time in degrees. We can divide it by 15 to get our local siderial time in hours, but often we leave the figure in degrees. The approximation is within 0.3 seconds of time for dates within 100 years of J2000.

HOUR ANGLE(HA)

We can build in the Earth's rotation by replacing the RA by the Hour Angle. The HA of an object increases with siderial time, but the declination stays the same, as the DEC measures the angle from the Earth's equator. We calculate the HA in degrees, so that we can take sines and cosines later.

A can be calculated using the following formula

If HA negative, we should add 360 to bring in range 0 to 360. RA must be in degrees.

	sin(ALT) = sin(DEC)*sin(LAT)+cos(DEC)*cos(LAT)*cos(HA)
	ALT = asin(ALT)

	cos(AZ)   =  sin(DEC) - sin(ALT)*sin(LAT)/ cos(ALT)*cos(LAT)
	AZ = acos(A)

If sin(HA) is negative, then AZ = A, otherwise AZ = 360 - A

Making the Machine understand

All the calculations we've done here so far are all in degrees. The problem with this is that even though it's easy to understand and convey this to others, the machine doesn't understand this. Here we used stepper motor. And for a stpper motor we have to calculate the steps. One step of a stepper is taken as 1.8 degrees.

1.8 degrees = 1 step

For more accuracy we can use microstepping. Here we used microstepping of 1/16
i.e, 1.8 / 16 = 0.1125
Therefore, for calculating the number of steps, we use the following formula.

Number of steps = no : of degrees/0.1125
This is the step equation

Design

Final Assembly

My awesome team's group project page can be found - here